“Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding.”– William Paul Thurston
The study of Mathematics at Westhoughton high school has been designed to empower students to become independent, methodical learners, with the aim of becoming analytical, critical thinkers who can tackle problems logically whilst deepening their enjoyment of mathematics and developing a curiosity for the world around us.
Mathematics at Westhoughton High School will explore connections between the different areas of Maths and other STEM subjects. We believe that to understand the development of mathematics through its history will help students with the contemporary applications and appreciate and respect the role mathematics plays in our lives.
Maths is so much more than numeracy! Mathematics has changed the world that we live in, we look after each other by considering topics such as: how mathematics forms the basis for all of our monetary systems and controls the way in which countries interact and exchange financially; how it helps us to create the latest blockbuster computer games, life-saving medical magnetic resonance imaging and the impact it will have on future technological and scientific breakthroughs.
We designed the mathematics curriculum with the intent of building upon prior knowledge to deepen understanding and prepare students to apply mathematical concepts to the outside world. The curriculum is ambitious but offers enrichment opportunities such as school trips, UKMT maths challenge, artful maths club and historical maths weeks where we have designed pictures using coding and even painted our own Fibonacci inspired frogs.
We want students to aim high and be inquisitive about maths whilst at the same time appreciating what skills they will need in their futures. We want all our learners to feel confident to use numbers in everyday problems in a world that is evolving, changing and developing exponentially. We want our students to never stop learning and increasing their enthusiasm for mathematics as it can help them with the necessary skills and determination to embrace the challenges and new ideas of the future.
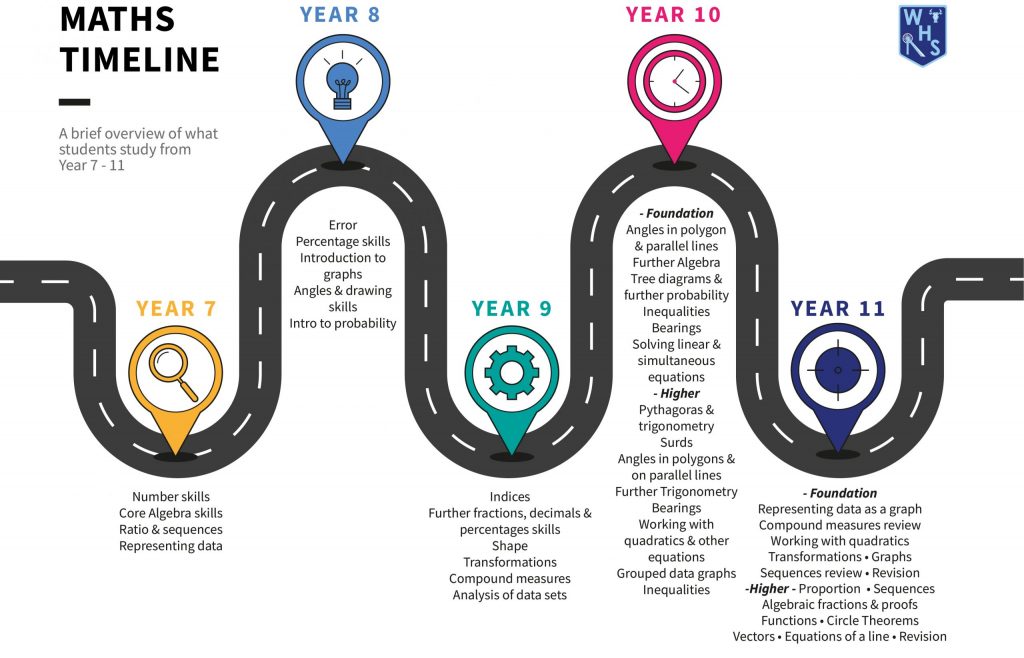
Please see parental overview timeline of the course in KS3 and KS4 below:
Links for Support/Help at Home
- Numeracy Practice together, even the times table to develop mental maths
- Use of accounts from school such as: Sparkx Maths, MathsWatch, Numeracy Ninjas, Corbett Maths and Seneca
- Help with measuring in the home (ingredients on recipes through to measuring within DIY)
- Support during weekly homework
- Correspondence with class teacher through Synergy, especially after data entries or assessments for additional personalised support
- Attend any workshops or parent-teacher offers from the Maths department to support core numeracy
- Use of Apps on tablets/phones that support numeracy, search ‘numeracy’ within the App store for a range of free apps to spend 10 minutes a day on
- Encouragement, the biggest blocker to our students developing their maths is their mindset that they ‘can’t do Maths’ – help us change that mindset
- Any study guides (available to loan from the library)
- Reading: books of famous mathematicians or the greater study of numbers
- Use of additional homework booklets, therapy work packs and/or additional resources from the class teacher via Synergy
- Use of student resources located within WHS SharePoint for students
- Participation in numeracy competitions in school alongside enrichment and extra-curricular clubs

